任何数除以0为何在数学上没有意义？会发生怎样的逻辑混乱

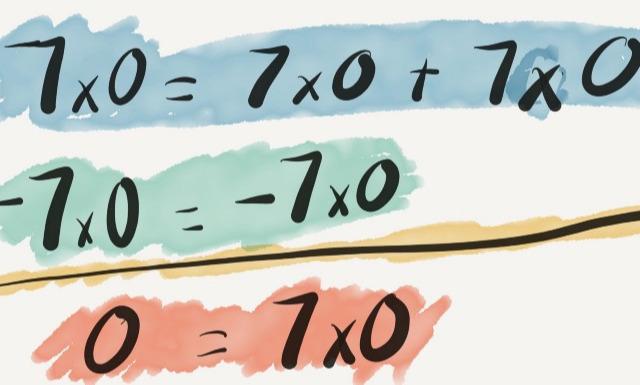
在数学的广阔天地里，有一条看似简单却引发无数争议的禁令：任何数除以0都是没有意义的。这条禁令如同一道无形的屏障，将我们熟悉的运算世界与一个充满悖论和混乱的数学禁地隔离开来。那么，究竟是什么原因让数学家们如此坚决地拒绝这一看似简单的计算呢？

要理解这个问题，我们首先需要回到除法的本质。在数学中，除法被定义为乘法的逆运算。换句话说，当我们说a除以b等于c时，实际上是在寻找一个数c，使得c乘以b等于a。这个定义看似简单，却蕴含着深刻的逻辑。

当我们将0作为除数时，这个简单的定义开始瓦解。考虑1除以0的情况。根据除法的定义，我们需要找到一个数c，使得c乘以0等于1。然而，根据乘法的基本性质，任何数乘以0都等于0。这意味着，无论我们选择什么值作为c，都无法满足这个等式。因此，1除以0在数学上是没有意义的。

更糟糕的是，如果我们尝试赋予1除以0一个值，比如无穷大（记为∞），我们会陷入更深的逻辑泥潭。根据乘法的逆运算性质，我们可能会认为0乘以∞应该等于1。然而，这与0乘以任何数都等于0的基本规则相矛盾。这种矛盾不仅破坏了数学的逻辑一致性，还可能导致一系列荒谬的结论，如“∞+1=∞”、“∞-∞=不确定”等。

数学家们之所以如此坚决地禁止除以0，正是为了保护数学体系的完备性和一致性。在实数系统中，每一个有理数和无理数都应该在实数轴上找到对应的位置，且不存在任何“空洞”。如果允许1除以0等于无穷大，就意味着我们需要在实数轴上引入一个代表无穷大的点。然而，这个点既无法与其他实数进行有序排列，又会破坏实数系统的连续性和完整性。

尽管在实数范围内，1除以0被严令禁止，但这并不妨碍数学家们在更广阔的数学领域中寻找答案。在复数系统、超限数理论以及非标准分析等高级数学分支中，无穷大被赋予了更为严谨的定义和运算规则，使得在特定条件下处理类似“1除以0”的问题成为可能。

例如，在复数系统中，通过引入虚数单位i（i²=-1），可以定义出一个被称为“虚无穷大”的概念，它能够参与到某些特定的运算中，而不会引发实数系统中的悖论。而在超限数理论中，通过构建包含所有有限数和无穷大的集合，如康托尔的超限数，可以对无穷大进行更为精细的分类和操作。

这些高级数学理论为我们提供了一种视角，即并非所有的“1除以0”都是不可接受的，关键在于如何在特定的数学框架下，妥善处理无穷大及其相关运算，以避免逻辑矛盾和系统不完备性。

在数学的世界里，“1除以0”并非一道无法逾越的鸿沟，而是一道激发我们深入理解数学本质、挑战既有认知边界的邀请函。或许有一天，随着数学理论的进一步发展，我们能以一种全新的方式理解和接纳这个看似禁忌的运算，将其纳入数学的宏伟殿堂，为人类认知世界的旅程增添新的光芒。