Excel 中计算加权平均数的套路公式

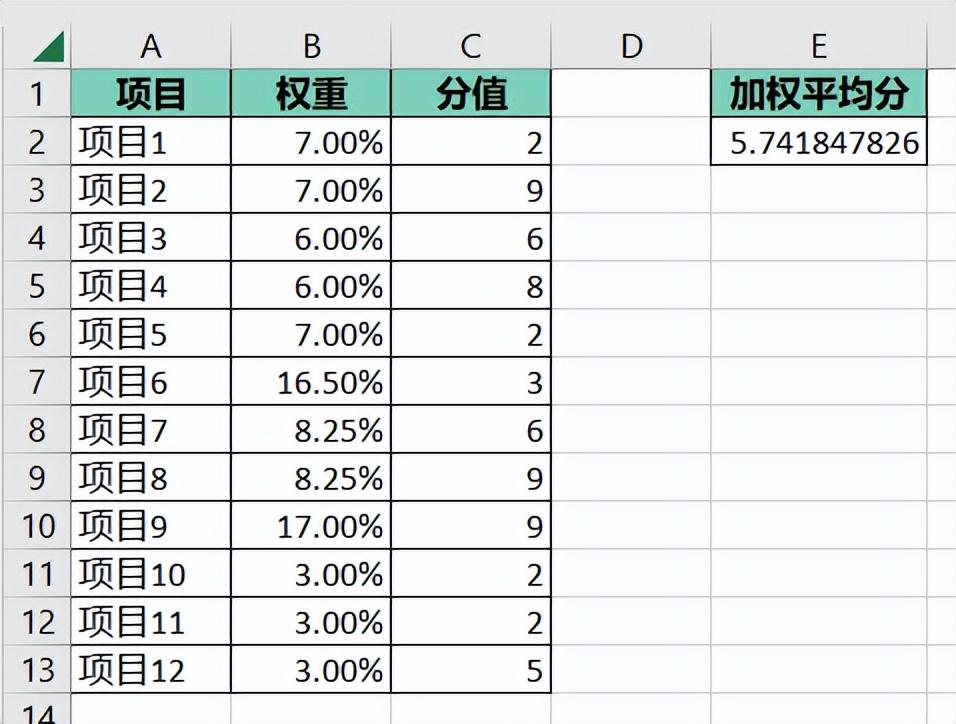
在日常生活中，我们经常需要计算平均数来反映一组数据的集中趋势。然而，当数据中某些数值的重要性不同时，简单平均数就无法准确反映实际情况。这时，加权平均数就派上了用场。

加权平均数是一种考虑了不同数值重要性的平均数计算方法。 它的计算公式是：加权平均数 = (数值1 × 权重1 + 数值2 × 权重2 + ... + 数值n × 权重n) / (权重1 + 权重2 + ... + 权重n)。其中，权重代表了每个数值在整体中的相对重要性。

让我们通过一个具体的例子来理解加权平均数的计算过程。假设小明在某门课程的平时测验中得了80分，期中考试得了90分，期末考试得了95分。学校规定，这三部分的成绩占比分别为20%、30%和50%。那么，小明的综合成绩就是：

(80 × 20% + 90 × 30% + 95 × 50%) / (20% + 30% + 50%) = 90.5分

相比之下，如果简单地将三次成绩相加再除以3，得到的平均分是88.33分。这个例子说明，加权平均数能够更准确地反映各个部分成绩的重要性。

加权平均数的应用非常广泛。在财务领域，它常用于计算加权平均成本、加权平均股价等。例如， 某投资者持有两只股票，股票A的股数为1000，价格为10元；股票B的股数为2000，价格为15元。 那么，该投资者持有的股票加权平均价格就是：

(1000 × 10 + 2000 × 15) / (1000 + 2000) = 13.33元

在教育领域，加权平均数常用于计算学生的综合成绩。在工作决策中，加权平均数可以帮助我们权衡不同意见的重要性。例如，如果老板对某项决策的权重是你的5倍，那么即使你给这项决策打60分，老板打100分，最终的加权平均分也会偏向老板的意见。

然而，加权平均数也有其局限性。首先，权重的设定往往带有主观性，不同的权重分配可能导致完全不同的结果。其次， 过度依赖加权平均数可能会忽视一些重要的非量化因素。 因此，在使用加权平均数时，我们需要谨慎考虑权重的合理性，并结合实际情况做出判断。

总的来说，加权平均数是一种强大的工具，能够帮助我们在面对复杂数据时做出更合理的判断。通过合理设置权重，我们可以突出重要数据的影响，从而获得更准确的平均值。在实际应用中，我们需要根据具体情况灵活运用加权平均数，同时也要意识到它的局限性，这样才能更好地发挥它的作用。