数学经典：阿基米德用一种非常直观的方法来计算椭圆的面积

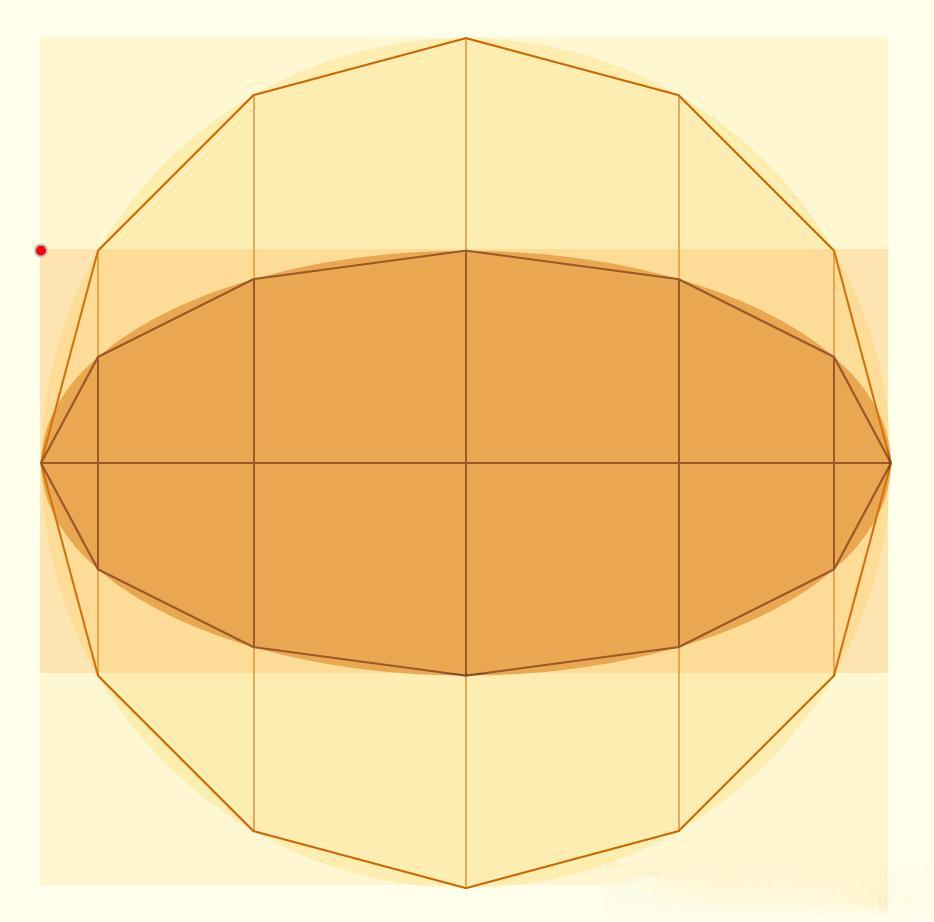
阿基米德在《关于圆锥体和球体》一书中提出了一个巧妙的方法来计算椭圆的面积。 他首先将椭圆视为垂直缩小的圆，然后利用圆的面积公式进行推广。具体来说，对于长半轴为a、短半轴为b的椭圆，其面积公式为：

这个公式是对圆面积公式的直观推广 ，体现了阿基米德深刻的几何洞察力。 他通过考虑椭圆和辅助圆内接的多边形，证明了椭圆面积与辅助圆面积之间的关系 ，从而推导出了椭圆面积的精确表达式。

相比之下， 现代数学家通常使用积分方法来计算椭圆面积。 以直角坐标系中椭圆的标准方程为例，其面积可以通过以下积分表达：

虽然这种方法在数学上更为严谨，但它失去了阿基米德方法所具有的直观性和几何美感。 阿基米德的方法不仅给出了椭圆面积的精确公式，更重要的是，它展示了如何通过几何直观来解决复杂的数学问题。

阿基米德的这种方法体现了古希腊数学家对直观几何思维的偏爱。 在缺乏现代代数工具的情况下，古希腊数学家们往往依赖于几何图形和直观论证来探索数学真理。阿基米德的椭圆面积计算方法正是这种思维方式的典范。

除了椭圆面积，阿基米德在数学领域的贡献还包括：

1. 圆的面积和周长的精确计算
2. 球体和圆柱体体积的计算
3. 螺旋线的研究
4. 杠杆原理的应用

这些成就使阿基米德被誉为“数学之神”，在数学史上占有极其重要的地位。

阿基米德的方法对后世数学发展产生了深远影响。它不仅为椭圆面积的计算提供了直观的几何视角，更重要的是，它展示了如何通过几何直观来解决复杂的数学问题。这种方法论影响了后世数学家的思维方式，为微积分学的诞生奠定了基础。

在当今这个高度抽象化的数学世界里，回顾阿基米德的方法提醒我们，数学不仅仅是符号和公式的堆砌，它更是一种直观的、富有创造性的思维活动。阿基米德的椭圆面积计算方法，就像一扇窗户，让我们得以窥见古希腊数学家们的智慧之光，也为我们今天的数学研究提供了宝贵的启示。