由一道周期函数判断题，分析判断周期函数的一般方法

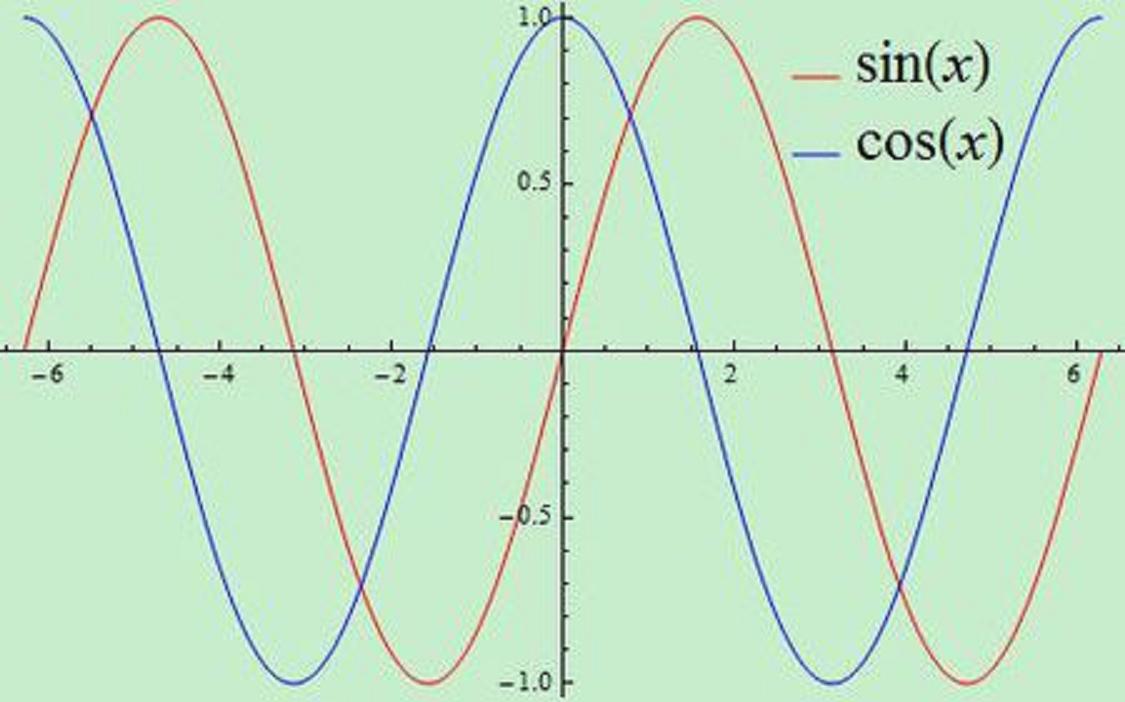
在数学的世界里，周期函数如同一首永不停歇的旋律，以其规律的重复性吸引着我们的注意。今天，让我们一起探讨如何判断一个函数是否具有这种迷人的周期性。

让我们从一个简单的例子开始：判断函数f(x) = sin(2x)是否为周期函数。直观上，我们知道正弦函数具有周期性，但如何严格地证明这一点呢？这就需要我们回到周期函数的定义。

周期函数的定义是：对于函数y = f(x)，如果存在一个非零常数T，使得当x取定义域内的每一个值时，都有f(x + T) = f(x)成立，那么我们就称f(x)为周期函数，T称为这个函数的一个周期。

回到我们的例子，我们需要找到一个T，使得sin(2(x + T)) = sin(2x)对所有x都成立。通过简单的代数运算，我们可以发现当T = π时，这个等式恒成立。因此，我们可以断定f(x) = sin(2x)是一个周期函数，其周期为π。

然而，并非所有函数都如此简单。对于更复杂的函数，我们可能需要采用不同的方法来判断其周期性。一种常用的方法是直接验证法，即尝试找到一个非零常数T，使得f(x + T) = f(x)恒成立。如果能找到这样的T，那么函数就是周期的；如果找不到，那么函数就不是周期的。

另一种方法是反证法。假设函数是周期的，然后试图推出矛盾。例如，要证明函数f(x) = ax + b（a ≠ 0）是非周期的，我们可以假设存在一个非零常数T使得f(x + T) = f(x)恒成立。这将导致a(x + T) + b = ax + b，进而得到aT = 0。由于a ≠ 0，这与T ≠ 0矛盾，因此我们可以断定f(x) = ax + b是非周期函数。

周期函数在数学和实际应用中扮演着重要角色。在信号处理中，周期信号的分析和处理是基础；在物理学中，许多自然现象如振动和波动都具有周期性；在工程学中，周期性运动的分析对于机械设计至关重要。因此，能够准确判断一个函数是否为周期函数，对于这些领域的研究和应用都具有重要意义。

判断函数周期性的关键在于理解周期函数的本质特征：函数值在定义域内有规律地重复出现。具体来说，我们可以关注以下几点：

1. 定义域：周期函数的定义域必须是至少一方无界的。
2. 周期性：寻找一个非零常数T，使得f(x + T) = f(x)恒成立。
3. 最小正周期：如果存在多个周期，那么最小的正周期是最基本的周期。
4. 周期函数的性质：了解周期函数的性质，如周期函数的和、差、积在一定条件下也是周期函数，可以帮助我们更快地做出判断。

总之，判断一个函数是否为周期函数需要我们深入理解周期函数的定义和性质，灵活运用各种判断方法，并结合具体的函数形式进行分析。通过不断的练习和思考，我们就能逐渐掌握这一技能，在数学的海洋中畅游，欣赏周期函数那美妙的旋律。