海伦公式及其推导过程

发布时间：2024-09-18

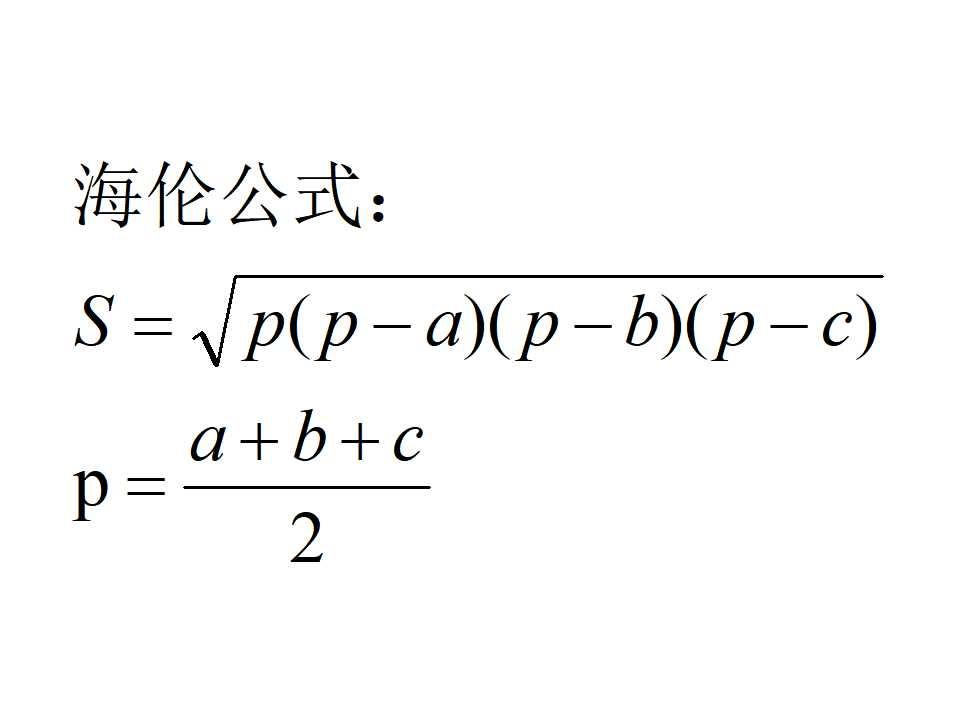
海伦公式是求解三角形面积的一个强大工具，它只需要知道三角形的三条边长就能计算出面积，而无需知道任何角度或高。这个公式的简洁性和实用性使其在几何学中占据重要地位。

海伦公式的推导过程虽然看似复杂，但实际上只需要运用一些基本的几何知识。让我们一步步来看这个推导过程：

首先，我们考虑一个任意的三角形ABC，其三边长分别为a、b、c。我们的目标是找到一个只包含这三条边长的表达式来表示三角形的面积。

我们从三角形的一个顶点（比如A）向对边BC作垂线，垂足为D。设BD=x，那么CD=b-x。
根据勾股定理，我们可以得到两个方程：h^2=b^2-(b-x)^2 和 h^2=c^2-x^2。这里h是垂线AD的长度，也就是三角形的高。
将这两个方程联立，消去x，我们可以得到一个关于h的方程。这个方程虽然看起来复杂，但通过一些代数变换，我们可以将其简化。
最终，我们得到三角形面积的表达式：S = 1/2 * a * h。但这个表达式仍然包含h，我们需要进一步化简。
通过引入半周长的概念，即p = (a+b+c)/2，我们可以将面积表达式进一步简化为： S = sqrt[p(p-a)(p-b)(p-c)] 。这就是著名的海伦公式。

这个推导过程展示了数学的美妙之处：从看似复杂的起点出发，通过一系列巧妙的变换，最终得到了一个简洁而强大的公式。海伦公式的实用性在于，它使得我们可以在不知道任何角度或高的情况下，仅凭三条边长就能计算出三角形的面积。

值得注意的是，海伦公式的推导过程虽然看似简单，但其中蕴含了深刻的数学思想。它不仅展示了勾股定理的应用，还体现了代数变换的技巧。这个公式的发现，标志着人类对几何学认识的一个重要进步。

在实际应用中，海伦公式被广泛应用于各种领域，从建筑设计到工程计算，甚至是天文学研究。它的简洁性和通用性使得它成为解决三角形面积问题的首选工具。

总的来说，海伦公式的推导过程不仅展示了数学的逻辑之美，也体现了数学在解决实际问题中的强大能力。它提醒我们，即使是最复杂的数学问题，也可能有一个简单而优雅的解决方案。