抛物线的通径是什么？用它可以简便解决这道高考数学题

抛物线的通径是一个重要的几何概念，它不仅体现了抛物线的对称性，还能在解决某些数学问题时发挥独特的作用。那么，什么是抛物线的通径呢？

通径是指过抛物线焦点且垂直于对称轴的直线与抛物线的两个交点之间的线段。这个定义看似简单，却蕴含着丰富的几何意义。根据抛物线的定义，焦点到准线的距离等于通径的一半，通常用p表示。因此，通径的长度为2p，这也是抛物线标准方程中2p的几何意义。

了解了通径的概念，我们来看看它在解决实际问题中的应用。以一道高考数学题为例：

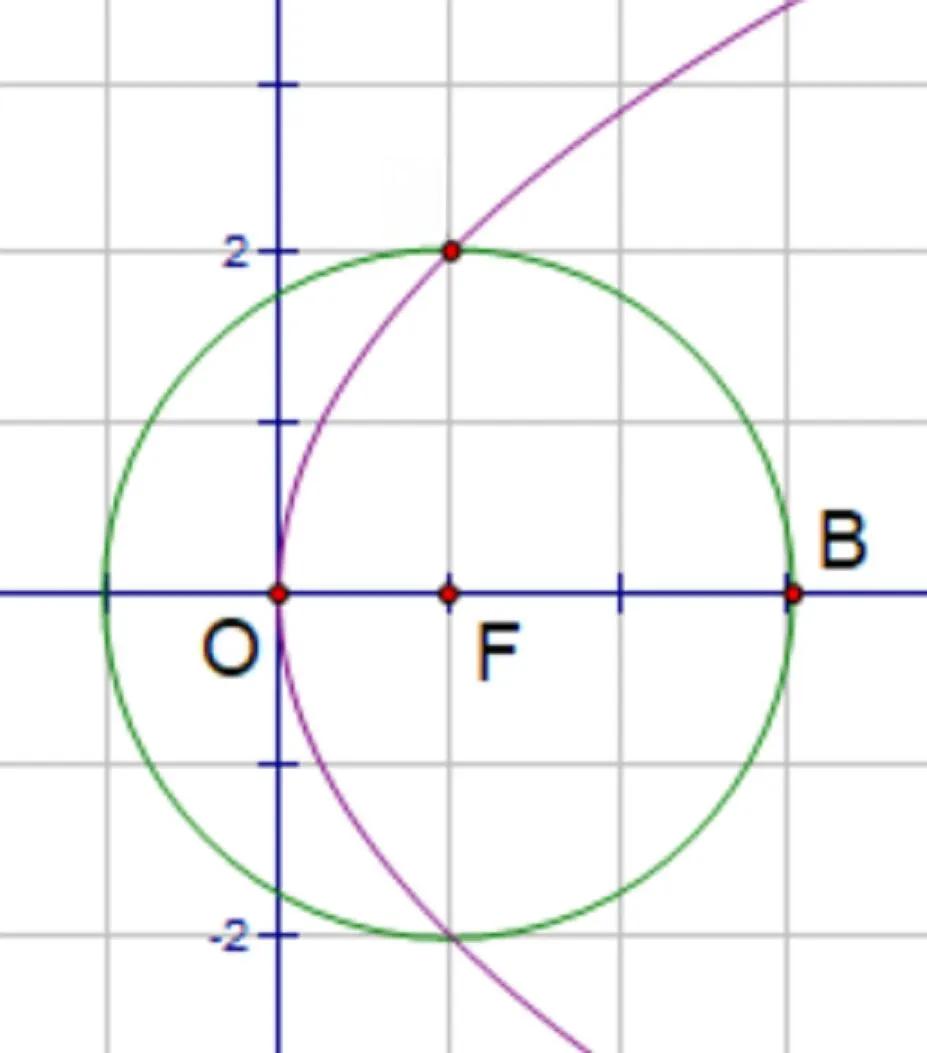
“已知抛物线y^2=4x的焦点为F，过F的直线与抛物线交于A、B两点，求线段AB的最小值。”

这道题看似复杂，但如果巧妙运用通径的概念，就能大大简化解题过程。首先，根据抛物线的标准方程y^2=4x，我们可以确定焦点F的坐标为(1,0)。接下来，考虑过焦点F且垂直于对称轴（即x轴）的直线。这条直线与抛物线的交点即为通径的两个端点。

由于通径的长度为2p，而给定的抛物线方程中2p=4，因此通径的长度恰好等于4。关键在于，通径是所有过焦点的弦中最短的一条。这意味着，无论直线AB如何倾斜，其长度都不会小于通径的长度。因此，线段AB的最小值就是通径的长度，即4。

这个例子展示了通径概念的强大之处。它不仅帮助我们直观地理解了抛物线的几何性质，还提供了一个简洁的解题方法。在处理涉及抛物线焦点和弦长的问题时，通径往往能成为解决问题的关键。

总的来说，抛物线的通径是一个简单而强大的几何概念。它不仅体现了抛物线的对称美，还在解决实际问题中发挥着重要作用。通过理解通径的概念和应用，我们可以更深入地把握抛物线的性质，提高解决几何问题的能力。