九年级数学丨反比例函数的性质

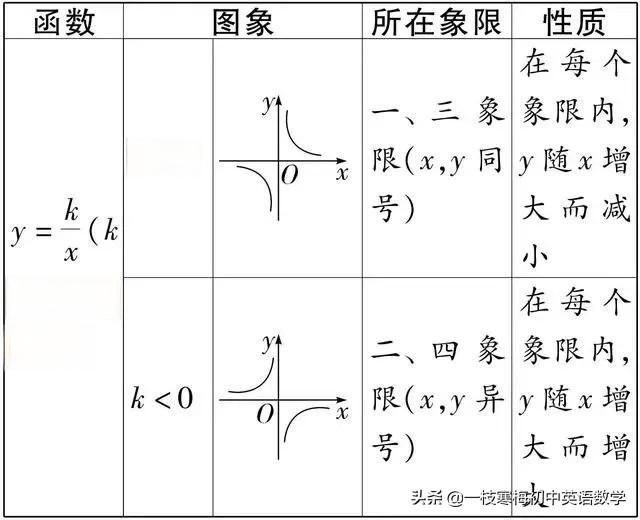
在九年级数学中，反比例函数是一个重要的知识点。它不仅是一种基本的数学模型，也是理解更复杂函数的基础。反比例函数的一般表达式为y=k/x，其中k是一个非零常数，称为反比例系数。

反比例函数图像特征与性质解析

反比例函数的图像是一条双曲线，具有以下显著特征：

1. 图像分布在第一、三象限或第二、四象限，取决于k的正负。当k>0时，图像位于第一、三象限；当k<0时，图像位于第二、四象限。

2. 图像关于原点对称。这意味着如果点（x，y）在图像上，那么点（-x，-y）也在图像上。

3. 图像无限接近但永远不会与x轴或y轴相交。这表明x和y的值可以无限接近0，但永远不会等于0。

4. 在每个象限内，图像表现出单调性。当k>0时，图像在第一、三象限内从左到右递减；当k<0时，图像在第二、四象限内从左到右递增。

反比例函数在实际生活中的应用举例

反比例函数不仅仅是一个数学概念，它在现实生活中也有广泛的应用。例如：

1. 在物理学中，两个物体之间的引力与它们质量的乘积成正比，与它们距离的平方成反比。这可以用反比例函数来表示。

2. 在经济学中，商品的价格和需求量之间往往存在反比例关系。当价格上升时，需求量通常会下降；反之亦然。

3. 在工程学中，一个项目的完成时间与参与工作的人员数量之间也存在反比例关系。增加工人数量可以缩短项目完成时间，但这种关系不是线性的。

掌握反比例函数学习方法与技巧

要学好反比例函数，可以采取以下方法：

1. 理解概念：首先，要深刻理解反比例函数的概念和表达式。记住y=k/x这个基本形式，并理解k的含义。

2. 掌握图像：熟悉反比例函数的图像特征，包括分布象限、对称性、渐近线等。可以通过绘制图像来加深理解。

3. 应用性质：学会在具体问题中应用反比例函数的性质，如单调性、对称性等。

4. 解决实际问题：尝试将反比例函数应用于实际问题中，如物理学中的引力问题、经济学中的供求关系等。

5. 练习题目：通过大量练习不同类型的问题，巩固所学知识。

6. 数形结合：学会用图形来解释和解决问题，这是数学中非常重要的思维方式。

掌握反比例函数不仅对当前的数学学习至关重要，也为未来学习更复杂的数学概念奠定了基础。通过理解其概念、熟悉其图像、应用其性质，并将其应用于实际问题中，学生可以更好地掌握这一重要知识点。记住，数学不仅仅是记忆公式，更重要的是理解背后的逻辑和应用。