中考数学——几何图形存在性问题解题策略汇编

发布时间：2024-09-19

在中考数学中，几何存在性问题一直是考生们的一大挑战。这类问题通常要求在给定的条件下，判断某种特定的几何图形是否存在，或者找出满足条件的点的位置。其中，等腰三角形的存在性问题尤为典型，它不仅能体现几何存在性问题的本质，还能引出一系列通用的解题策略。

等腰三角形存在性问题的两种解法

以一个简单的例子开始：已知线段AB，在平面内找一点C，使得△ABC为等腰三角形。这个问题看似简单，却蕴含了存在性问题的核心思想。

解决这个问题有两种主要方法：代数法和几何法。

代数法，也称为“盲解盲算法”，是一种通用的方法。它通过列出三角形三边的长度（或其平方），然后分类讨论并解方程来找到可能的解。对于等腰三角形，存在三种情况：AB=AC、BA=BC、CA=CB。这种方法虽然机械，但适用于各种存在性问题，尤其是当图形较为复杂时。

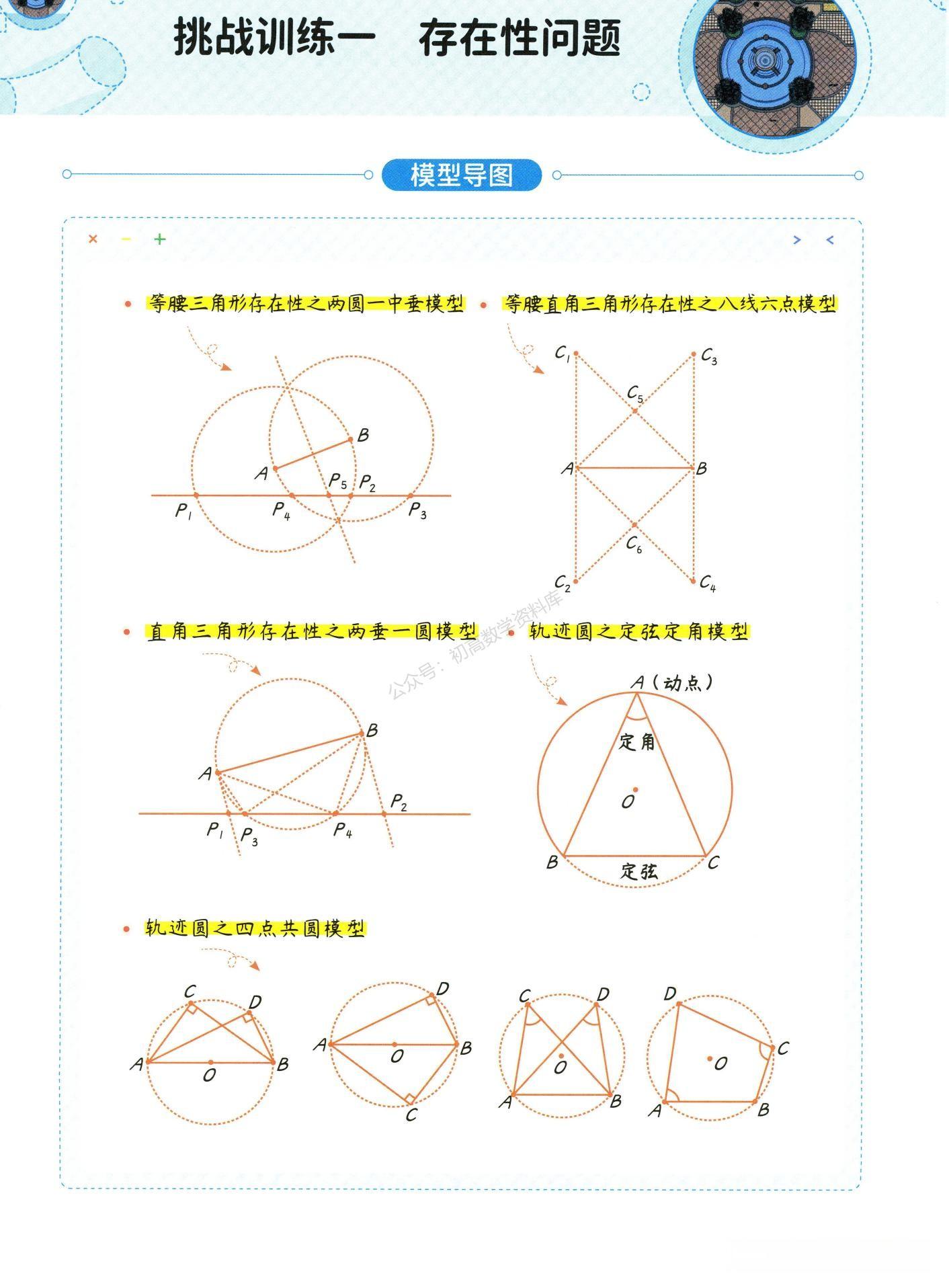
几何法，特别是“两圆一线”法，是一种更直观的方法。它基于等腰三角形的性质，指出满足条件的点C位于两个特定的圆和一条直线上。具体来说，这些点位于以A、B为圆心，AB长为半径的圆上，以及线段AB的垂直平分线上（除了与AB在同一直线上的点）。这种方法不仅给出了直观的图形描述，还为解决更复杂的存在性问题提供了思路。

解决几何存在性问题的通用策略

从等腰三角形存在性问题出发，我们可以总结出解决几何存在性问题的一些通用策略：

分类讨论：对于存在性问题，首先要考虑所有可能的情况。例如，在等腰三角形问题中，我们考虑了三种可能的等腰情况。
图形辅助：利用几何图形的性质和定理，如等腰三角形的性质、垂直平分线的性质等，来简化问题。图形辅助不仅能帮助我们直观地理解问题，还能启发我们找到更简洁的解法。
数形结合：将几何问题转化为代数问题，或者将代数问题可视化。例如，在等腰三角形问题中，我们可以将问题转化为求解方程组。
构造法：在某些情况下，直接证明存在性可能很困难。这时，我们可以尝试构造一个满足条件的图形或点，从而证明存在性。
反证法：对于否定的存在性问题，反证法是一个有力的工具。假设存在满足条件的图形或点，然后通过逻辑推理得出矛盾，从而证明不存在。
特殊化与一般化：从特殊情况入手，找到解题思路，然后推广到一般情况。或者，将问题一般化，找到更广泛的解题方法。
模型化：将问题转化为已知的数学模型，如等腰三角形模型、直角三角形模型等。熟悉常见的数学模型可以帮助我们更快地找到解题思路。
动态思维：考虑图形的变化过程，寻找不变量。在存在性问题中，常常需要在变化中寻找不变的元素，从而找到解题的关键。

通过深入理解等腰三角形存在性问题及其解法，我们可以更好地掌握解决几何存在性问题的技巧。记住，几何存在性问题不仅仅是关于图形的，更是关于逻辑思维和创造性解决问题的能力。通过不断的练习和思考，你将能够更自信地应对这类挑战。