阿基米德螺线是怎么被发明的？

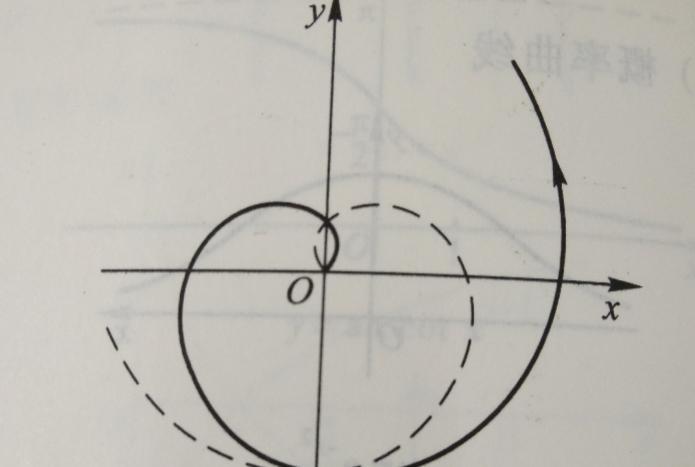
阿基米德螺线，这个看似简单的数学曲线，却蕴含着古希腊数学家的智慧，至今仍在现代科技中发挥着重要作用。让我们一起追溯它的起源，探索它的奥秘。

阿基米德螺线，又称为等速螺线，是一种特殊的螺旋曲线。它描述了一个点在匀速远离固定点的同时，又以固定角速度绕该点转动的轨迹。这种曲线的极坐标方程为r = a + bθ，其中a和b是常数，θ是极角。阿基米德螺线具有一个有趣的特性：在每个旋转周期内，曲线是等距离外扩的，因此又被称为等距螺旋。

这种曲线的发明可以追溯到公元前3世纪，由古希腊伟大的数学家阿基米德在其著作《螺旋线》中首次描述。阿基米德（公元前287年-公元前212年）是古希腊最杰出的科学家之一，他的贡献不仅限于数学领域，还涉及物理学、工程学等多个领域。阿基米德在亚历山大城求学期间，接触到了丰富的文化遗产，这为他日后的科学研究奠定了基础。

在古希腊时期，阿基米德螺线的应用主要体现在数学和物理学领域。阿基米德利用这种曲线解决了“化圆为方”这一古老的数学难题。通过构造阿基米德螺线，他证明了圆的周长可以等价于一个特定的直线段长度，从而实现了将圆的面积转化为一个具有相同面积的正方形。这一成就展示了阿基米德深刻的数学洞察力和创造力。

随着时间的推移，阿基米德螺线的应用范围不断扩大。在自然界中，我们可以在许多生物体上发现类似阿基米德螺线的结构，如某些螺类的外壳、植物的缠绕茎等。这种螺旋结构之所以在自然界中广泛存在，是因为它具有优良的力学性能，能够以最小的材料实现最大的结构强度。

在现代科技领域，阿基米德螺线的应用更是无处不在。在机械工程中，阿基米德螺线被用于设计各种传动装置和螺旋弹簧。在建筑设计中，这种曲线被用来优化结构的受力分布。在电子工程领域，阿基米德螺线天线因其良好的辐射特性而被广泛应用。

从数学角度来看，阿基米德螺线的发现标志着人类对曲线性质认识的深化。它不仅是一种几何图形，更是连接数学与物理世界的桥梁。阿基米德螺线的数学表达式为后来微积分的发展奠定了基础，预示了无穷小分析领域的兴起。

阿基米德螺线的发明和应用，充分体现了古希腊数学家的智慧和创造力。它不仅在当时解决了重要的数学和物理问题，而且在两千多年后的今天仍然发挥着重要作用。这再次证明了数学作为一门基础科学的永恒魅力和价值。