格林公式及其使用

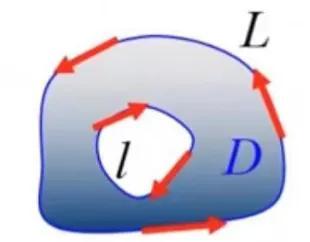
格林公式是数学中的一个重要工具，它建立了曲线积分与二重积分之间的联系。虽然这个公式看起来抽象复杂，但它在物理学和工程学中有着广泛而重要的应用。

在物理学中，格林公式被用来解决各种边界值问题。例如，在电磁学中，格林函数被用来描述一个“单位强度点源”所产生的“效果”。通过将分布源分割为多个点源的叠加，可以利用格林函数来计算整个源所产生的效果。这种方法不仅在数学上更为简洁优雅，也更容易从物理上理解。

格林公式的应用远不止于此。在工程学中，它被广泛应用于无线通信和电磁兼容等领域。例如，在无线通信中，格林函数被用来描述天线辐射的电磁场。通过计算格林函数，工程师们可以优化天线设计，提高通信效率。在电磁兼容领域，格林函数被用来分析和控制电磁干扰，这对于现代电子设备的设计至关重要。

格林公式的另一个重要应用是在计算区域面积方面。通过选取适当的函数L和M，使得Ldx + Mdy在闭合路径上的积分等于区域的面积，可以利用格林公式来计算平面图形的面积。这种方法不仅适用于规则图形，也适用于复杂的不规则区域。

格林公式的应用不仅限于二维空间。它是斯托克斯定理的二维特例，而斯托克斯定理则将曲线积分与曲面积分联系起来。这意味着格林公式的思想可以推广到更高维度的空间，为解决更复杂的问题提供了有力的工具。

尽管格林公式在数学上看起来可能有些抽象，但它的实际应用却非常广泛和重要。从电磁学的基本理论到现代通信技术的设计，格林公式都在发挥着关键作用。它不仅是一个数学工具，更是连接理论与实践的桥梁，帮助我们更好地理解和改造世界。