复数几何意义是不是值得了解？

复数，这个由实部和虚部组成的数学概念，长期以来被认为是“虚幻”的存在。然而，正是这种看似抽象的数学工具，在现代科技中扮演着不可或缺的角色。复数的几何意义，更是为我们打开了一扇通往复杂世界的大门。

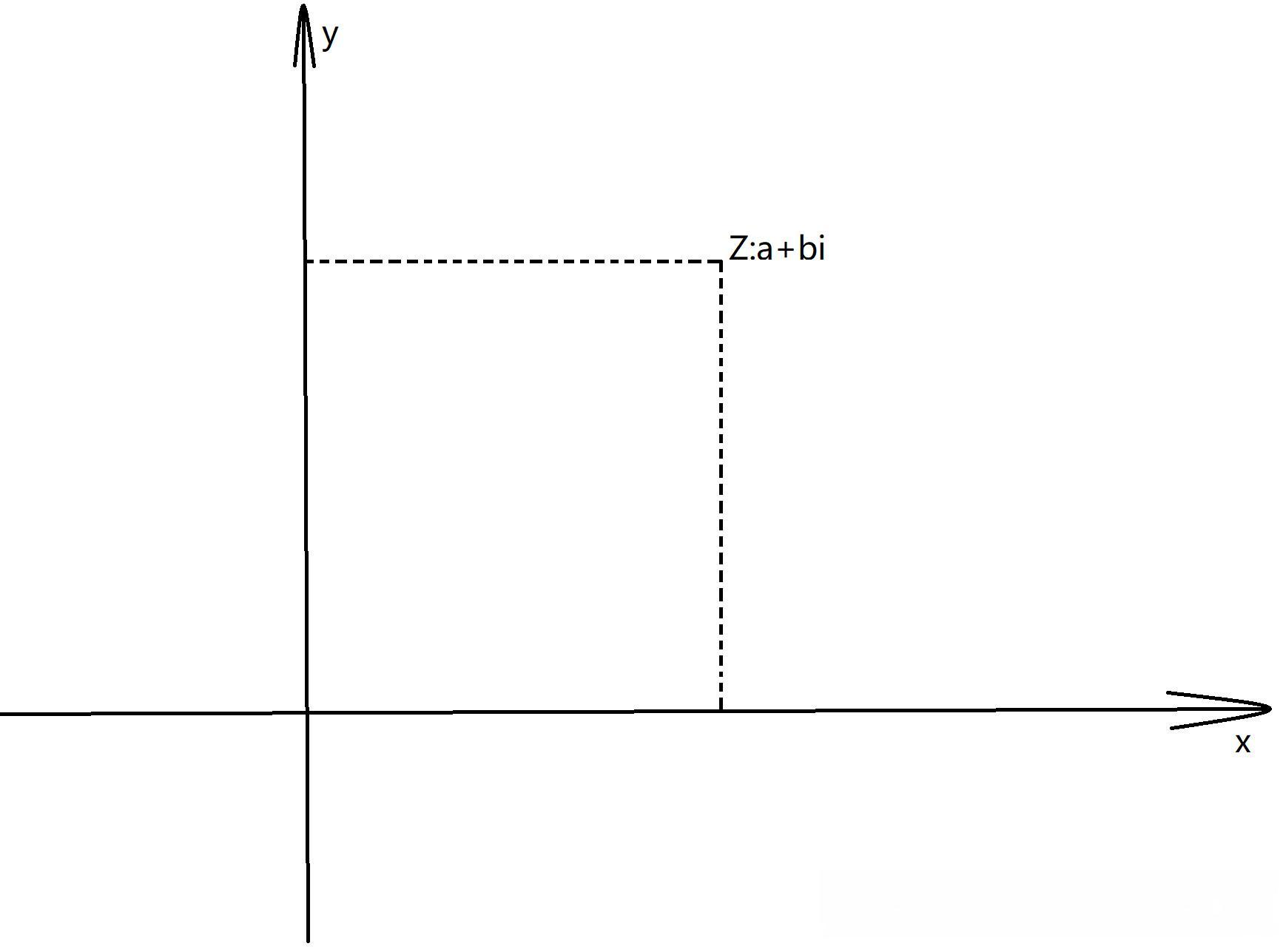
复数的几何表示最早可以追溯到19世纪初。德国数学家高斯发明了复数平面，将复数表示为平面上的点。这种表示方法不仅直观地展示了复数的代数和几何性质，更为复数在各个领域的应用奠定了基础。

在信号处理领域，复数的几何意义尤为重要。傅里叶变换，这个将信号从时域转换到频域的强大工具，本质上就是在复数域中进行的运算。通过复数，我们可以将复杂的信号分解为不同频率的组成部分，这对于音频处理、图像处理以及通信技术等领域至关重要。

电路理论中，复数的应用同样广泛。在交流电路分析中，电压和电流通常用复数来表示，因为这样可以方便地处理相位差问题。通过使用复数，工程师能够更简单地分析和设计复杂的电路系统。

量子力学中，复数更是扮演着核心角色。波函数，这个描述粒子量子状态的数学对象，就是用复数表示的。波函数的模平方给出了粒子出现在某位置的概率，这一描述方式使得量子力学的预测成为可能。

复数的几何意义不仅体现在其应用上，更深刻地反映了数学与现实世界的联系。正如维也纳量子光学和量子信息研究所的物理学家所展示的，量子理论的某些预测只能用包含复数的理论来描述。这一发现不仅证实了复数在量子理论中的必要性，也暗示了复数可能揭示了自然界更深层次的规律。

复数的发展历程也颇具启发性。从最初被数学家们视为“虚幻之数”，到如今成为现代科技的基石，复数的演变反映了人类认知的不断深化。它告诉我们，看似抽象的数学概念，往往蕴含着深刻的实际应用价值。

复数的几何意义，不仅为我们提供了解决复杂问题的工具，更拓展了我们对世界的认知。它将抽象的数学概念与直观的几何表示相结合，为我们理解自然界提供了一个全新的视角。因此，了解复数的几何意义，不仅是数学学习的需要，更是理解现代科技、探索自然奥秘的必经之路。