为什么圆的面积的导数等于周长？球的的体积的导数等于其表面积？| 第四届数学文化征文

圆的面积导数等于周长，球的体积导数等于表面积——这一数学现象不仅令人惊讶，更蕴含着深刻的数学原理。

让我们先回顾一下这两个公式：

圆的面积公式为 (S = \pi r^2)，其导数为 (S' = 2\pi r)，恰好等于圆的周长。

球的体积公式为 (V = \frac{4}{3}\pi r^3)，其导数为 (V' = 4\pi r^2)，恰好等于球的表面积。

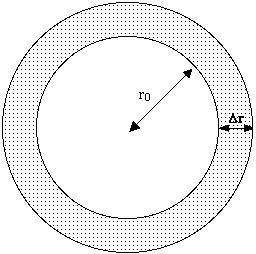
为什么会出现这种奇妙的对应关系？关键在于导数的几何意义。导数描述的是函数在某一点的变化率，即当自变量（在这个问题中是半径 (r)）发生微小变化时，函数值（面积或体积）的变化量。当我们增加圆的半径时，增加的面积实际上是一个薄薄的圆环；当增加球的半径时，增加的体积实际上是一个薄薄的球壳。这两种情况下，增加的量都可以近似看作是一个矩形或柱体的面积或体积，其长或底面积恰好是原来的周长或表面积。

这种对应关系并非仅限于圆和球。事实上，对于任何由半径确定大小的几何图形，其面积（或体积）关于半径的导数都等于其周长（或表面积）。例如，对于一个半径为 (r) 的正方形，其面积为 (S = 4r^2)，导数 (S' = 8r) 正好等于其周长。这种普遍性反映了数学中的一致性和简洁性。

这一现象不仅有趣，更有重要的数学意义和应用价值。在物理学中，它可以帮助我们理解电荷分布与电势的关系。例如，如果一个球形电荷分布的电荷密度与半径成正比，那么其电势关于半径的导数恰好等于球面上的电荷密度。这种对应关系简化了物理问题的求解过程。

更深层次地，这一现象体现了微积分与几何的紧密联系。它展示了导数不仅是一个抽象的数学概念，更有着直观的几何解释。这种联系使得我们能够用微积分的方法来解决几何问题，反之亦然。

最后，这一现象展示了数学的美妙之处。它揭示了看似不相关的概念（面积与周长、体积与表面积）之间的内在联系，体现了数学结构的和谐统一。这种美不仅存在于抽象的数学理论中，更体现在我们日常生活中随处可见的几何形状中。

圆的面积导数等于周长，球的体积导数等于表面积——这不仅仅是一个数学巧合，更是数学世界中一个精妙绝伦的设计。它提醒我们，在探索数学奥秘的过程中，要时刻保持好奇心和洞察力，因为最简单的公式中可能蕴含着最深刻的真理。