人工智能之概率论基础：如何使用韦恩图来判断事件之间的关系？

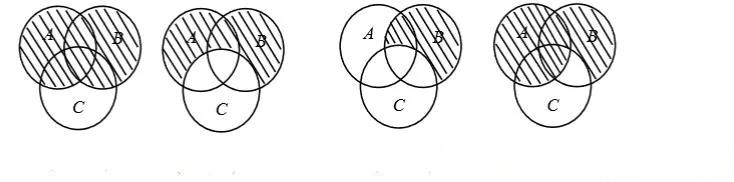
韦恩图（Venn Diagram）是一种直观的可视化工具，通过重叠的圆形来展示集合之间的关系。它不仅在数学、统计学和逻辑学中广泛应用，更是解决概率问题的有力武器。

让我们通过一个简单的概率问题来了解韦恩图的应用。假设在一个班级里，有30%的学生喜欢数学，40%的学生喜欢英语，同时有20%的学生既喜欢数学又喜欢英语。现在随机选择一名学生，求他既喜欢数学又喜欢英语的概率。

要解决这个问题，我们可以使用韦恩图来直观地展示这些信息。首先，我们画两个相交的圆，一个代表喜欢数学的学生，另一个代表喜欢英语的学生。然后，根据题目信息，在重叠区域标注20%，在只喜欢数学的区域标注10%（30%-20%），在只喜欢英语的区域标注20%（40%-20%）。最后，计算既喜欢数学又喜欢英语的概率，即20%除以总人数100%，得到答案是0.2。

这个例子展示了韦恩图在解决概率问题中的强大功能。它不仅帮助我们清晰地组织信息，还能直观地展示集合之间的关系，使复杂的概率问题变得简单易懂。

韦恩图的应用远不止于此。在商业领域，它可以用来比较和对比不同的产品、营销策略或设计方案。例如，一家公司可以使用韦恩图来分析三种不同产品的特点，找出它们的共同点和差异点，从而制定更有效的市场策略。

在教育领域，韦恩图同样大有用武之地。老师可以用它来比较两个历史事件、文学作品或科学概念，帮助学生更好地理解和记忆知识。例如，通过韦恩图比较《红楼梦》和《西游记》中的人物特点，学生可以更直观地看到两部作品的异同。

绘制韦恩图并不复杂。以两个集合为例，我们只需要画两个相交的圆，然后在不同的区域标注相应的信息。如果涉及三个集合，可以画三个相交的圆，形成更多的重叠区域。对于更复杂的场景，还可以使用三维韦恩图或按比例绘制的韦恩图，以适应不同的比较需求。

韦恩图的简单性和直观性使其成为一种强大的工具。它不仅能帮助我们解决概率问题，还能应用于各种比较和分析场景。无论是在学术研究、商业决策还是日常生活中，韦恩图都能帮助我们更清晰地理解事物之间的关系，做出更明智的选择。