三维Mesh网格的体积计算算法及JS代码

三维Mesh网格是计算机图形学中表示三维物体的一种常见方式。计算Mesh网格的体积是一个基本但重要的问题，在许多领域都有应用，如计算机辅助设计（CAD）、3D打印和游戏开发等。本文将介绍一种简单而有效的方法来计算三维Mesh网格的体积，并给出JavaScript代码实现。

Mesh网格体积计算原理

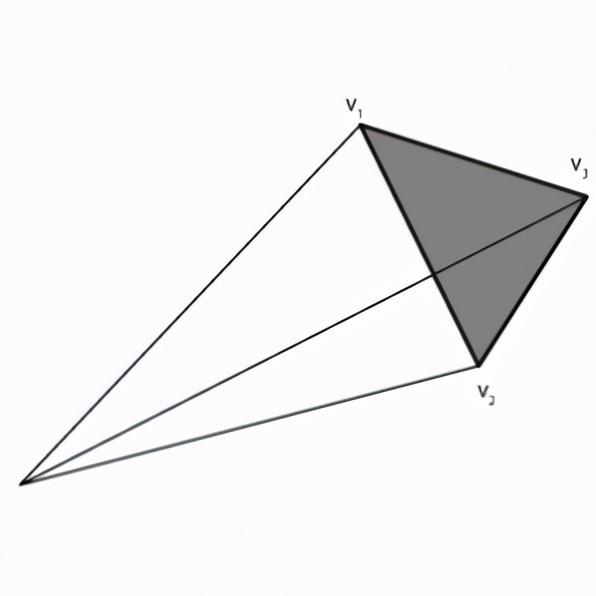
计算Mesh网格体积的基本思路是将网格分解为多个三角面，然后计算每个三角面对应的四面体体积，并将这些体积累加起来。 一个三角形本身没有体积，因此我们实际上是计算从原点到三角面的四面体体积。

给定三角形的三个顶点v1、v2和v3，四面体的体积可以通过以下公式计算：

V = (1/6) * (v1 × v2) · v3

其中“×”表示向量叉乘，“·”表示向量点乘。这个公式实际上是计算一个3×3矩阵行列式的六分之一，而这个矩阵的每一行代表一个顶点。除以6是因为行列式实际上表示了由三个向点形成的平行六面体的体积，而我们可以将6个四面体塞进这个平行六面体中。

值得注意的是， 这些体积是有符号的，具体取决于顶点的顺序。 如果顶点按照顺时针或逆时针顺序排列（相对于观察者的视角），得到的体积可能是正的或负的。面向远离原点方向的三角形对应的四面体体积将被加到总体积中，而面向原点方向的三角形对应的四面体体积将被从总体积中减去。这种有符号体积的累加确保了最终得到的是Mesh网格的净体积。

JavaScript代码实现

基于上述原理，我们可以编写如下的JavaScript代码来计算Mesh网格的体积：

var volume = 0;
var v1 = vec3.create(),
    v2 = vec3.create(),
    v3 = vec3.create();
var i, index1, index2, index3;

for (i = 0; i < numIndices; ) {
  index1 = indices[i++] * 3;
  index2 = indices[i++] * 3;
  index3 = indices[i++] * 3;

  vec3.set(v1, vertices[index1], vertices[index1 + 1], vertices[index1 + 2]);
  vec3.set(v2, vertices[index2], vertices[index2 + 1], vertices[index2 + 2]);
  vec3.set(v3, vertices[index3], vertices[index3 + 1], vertices[index3 + 2]);

  vec3.cross(v1, v1, v2);
  volume += vec3.dot(v1, v3);
}

volume = Math.abs(volume / 6.0);

在这段代码中， numIndices 是网格中三角形的数量， indices 是一个包含所有三角形顶点索引的数组， vertices 是一个包含所有顶点坐标的数组。 vec3 是一个用于向量操作的库，提供了 create 、 set 、 cross 和 dot 等方法。

优化计算效率

对于由大量相同或相似部件组成的复杂对象，直接计算每个三角面的体积可能会非常耗时。 在这种情况下，我们可以利用体积的旋转不变性和平移特性来优化计算。

具体来说， 我们可以计算每个三角形的“一般体积”，这是一个与三角形位置无关的向量。 对于每个三角形，我们可以计算如下三个分量：

Vx = y2z3 - y1z3 + y1z2 - y3z2 + y3z1 - y2z1
Vy = x1z3 - x2z3 + x3z2 - x1z2 + x2z1 - x3z1
Vz = x1y2 - x2y1 + x3y1 - x1y3 + x2y3 - x3y2

然后，对于整个Mesh网格，我们可以计算其“一般体积”向量V = (Vx, Vy, Vz)。对于任意平移(xt, yt, zt)，Mesh网格的体积可以通过以下公式快速计算：

Vt(xt, yt, zt) = V + Vx * xt + Vy * yt + Vz * zt

这种方法不仅大大减少了计算量，而且不需要知道每个部件的具体位置和方向。

结论

计算三维Mesh网格的体积是一个看似简单但实际应用广泛的问题。通过将网格分解为三角面，并计算每个三角面对应的四面体体积，我们可以得到网格的总体积。这种方法不仅简单直观，而且可以很容易地在各种编程语言中实现。对于由大量重复部件组成的复杂对象，我们还可以通过计算“一般体积”来进一步优化计算效率。这种体积计算方法在计算机图形学、3D打印等领域有着广泛的应用。