对全连接层的通俗理解

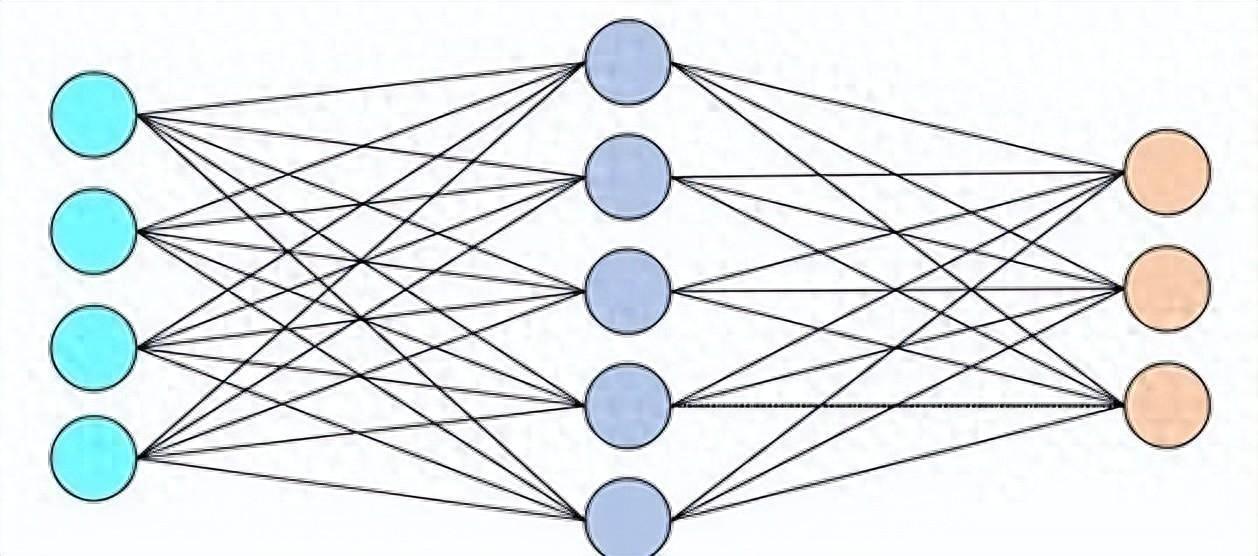
全连接层（Fully Connected Layer，简称FC层）是神经网络中的一种基本层类型 ，通常位于网络的最后几层。它的特点是每一个神经元都与前一层的每一个神经元相连接，这种连接方式使得每个输入都影响每个输出。

想象一下，全连接层就像一个复杂的投票系统。 每个输入特征都相当于一个选民，而每个输出节点则是一个候选人 。每个选民都有权对每个候选人进行投票，而投票的权重则由连接它们的权重值决定。最终，每个候选人的得票数就是所有选民投票的加权和。

全连接层的主要作用是将前面提取到的特征综合起来，实现从特征空间到类别空间的映射 。在分类任务中，全连接层通常作为网络的最后一层，直接将全连接层的维度设为类别数量或通过Softmax函数输出每个类别的概率分布，从而实现对输入数据的分类。

从数学角度来看，全连接层的计算过程可以表示为一个简单的矩阵乘法。假设输入向量为x，权重矩阵为W，偏置向量为b，激活函数为f，则输出向量y可以表示为：y = f(Wx + b)。这里的f可以是ReLU、Sigmoid、Tanh等非线性函数，用于增加模型的表达能力。

在卷积神经网络（CNN）中，全连接层通常位于多个卷积层和池化层之后。这种结构使得CNN能够先从图像中提取局部特征，然后再通过全连接层将这些特征整合起来进行分类。例如，在手写数字识别任务中，前面的卷积层和池化层可能已经提取出了数字的边缘、拐角等局部特征，而全连接层则负责将这些局部特征组合成完整的数字形状。

值得注意的是， 全连接层的参数量通常非常大 。以一个简单的例子来说，如果输入向量的维度为100，输出向量的维度为10，那么权重矩阵W的大小就是100x10，再加上10个偏置项，总共有1010个参数。这也就是为什么全连接层通常位于网络的最后几层，因为过早使用全连接层会导致参数量过大，容易造成过拟合。

在实际应用中，全连接层可以通过不同的方式实现 。例如，在PyTorch中，可以使用nn.Linear类来创建一个全连接层。以下是一个简单的例子：

import torch
import torch.nn as nn

class SimpleNN(nn.Module):
    def __init__(self, input_size, num_classes):
        super(SimpleNN, self).__init__()
        self.fc1 = nn.Linear(input_size, 64)  # 第一个全连接层
        self.fc2 = nn.Linear(64, 32)  # 第二个全连接层
        self.fc3 = nn.Linear(32, num_classes)  # 输出层，维度为类别数量

    def forward(self, x):
        x = torch.relu(self.fc1(x))  # ReLU激活函数
        x = torch.relu(self.fc2(x))
        x = self.fc3(x)  # 最后一层不需要激活函数，因为我们会在损失函数中应用Softmax
        return x

在这个例子中，我们定义了一个包含三个全连接层的简单神经网络。输入向量的维度为input_size，输出向量的维度为num_classes。通过这种方式，我们可以轻松地在PyTorch中实现和训练包含全连接层的神经网络模型。