无理数被发现的过程曲折，他的研究推动数学发展，自己却被处死

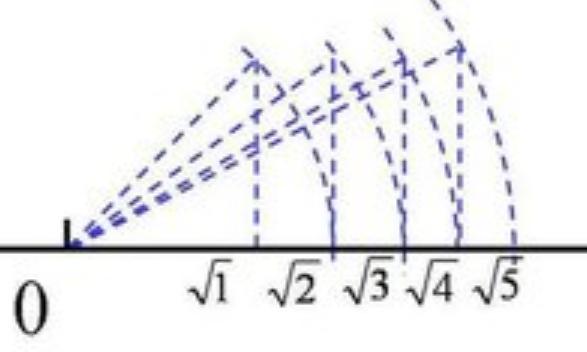
公元前5世纪，古希腊数学家希帕索斯发现了一个惊人的事实：等腰直角三角形的直角边与其斜边的长度比，无法用整数或分数表示。这个简单的几何事实，直接挑战了当时主导西方数学界的毕达哥拉斯学派的核心信条——“万物皆数”。

毕达哥拉斯学派认为，宇宙间的一切现象都能归结为整数或整数之比。然而，希帕索斯的发现揭示了一个全新的数学世界——无理数的存在。这个发现不仅违背了毕达哥拉斯派的信条，更冲击了当时希腊人普遍持有的“一切量都可以用有理数表示”的信仰。

面对这一挑战，毕达哥拉斯学派陷入了恐慌。传说中，希帕索斯因为这一发现而被学派成员投进大海，处以“淹死”的惩罚。这个残酷的故事，生动地展现了当时人们对这一数学发现的恐惧和抵触。

希帕索斯的悲剧并没有阻止真理的传播。相反，它引发了数学史上著名的第一次数学危机。这场危机持续了大约30年，直到公元前370年左右，以无理数的定义出现为结束标志。

为了解决这场危机，柏拉图的学生攸多克萨斯（Eudoxus）提出了一个新的比例理论。他巧妙地处理了可公度和不可公度的问题，为无理数的存在提供了逻辑基础。这一理论后来被收录在欧几里得的《几何原本》中，成为数学发展的重要里程碑。

无理数的发现对数学发展产生了深远的影响。首先，它推动了数学从经验科学向演绎科学的转变。古希腊人开始意识到，直觉和经验并不总是可靠的，而推理证明才是数学的基石。这种认识直接促成了欧几里得几何公理体系的建立，为数学的发展奠定了坚实的基础。

其次，无理数的发现极大地丰富了数学的内容。数学家们开始正式研究无理数，最终提出了包含有理数和无理数的新的数类——实数，并建立了完整的实数理论。这一理论为后来数学分析的发展奠定了基础。

最后，无理数的发现改变了人们对数学本质的认识。它打破了人们对整数和有理数的崇拜，让人们认识到数学世界的无限性和复杂性。这种认识促进了数学思想的解放，为后来数学的进一步发展开辟了道路。

从希帕索斯的悲剧到无理数理论的建立，我们看到了数学发展过程中真理与传统、创新与保守之间的激烈碰撞。无理数的发现不仅推动了数学的进步，也深刻影响了人类对世界的认知。它告诉我们，追求真理的道路虽然曲折，但最终必将通向光明。