什么是欧拉公式?欧拉公式保姆级证明推导,学会立刻提升数学能力

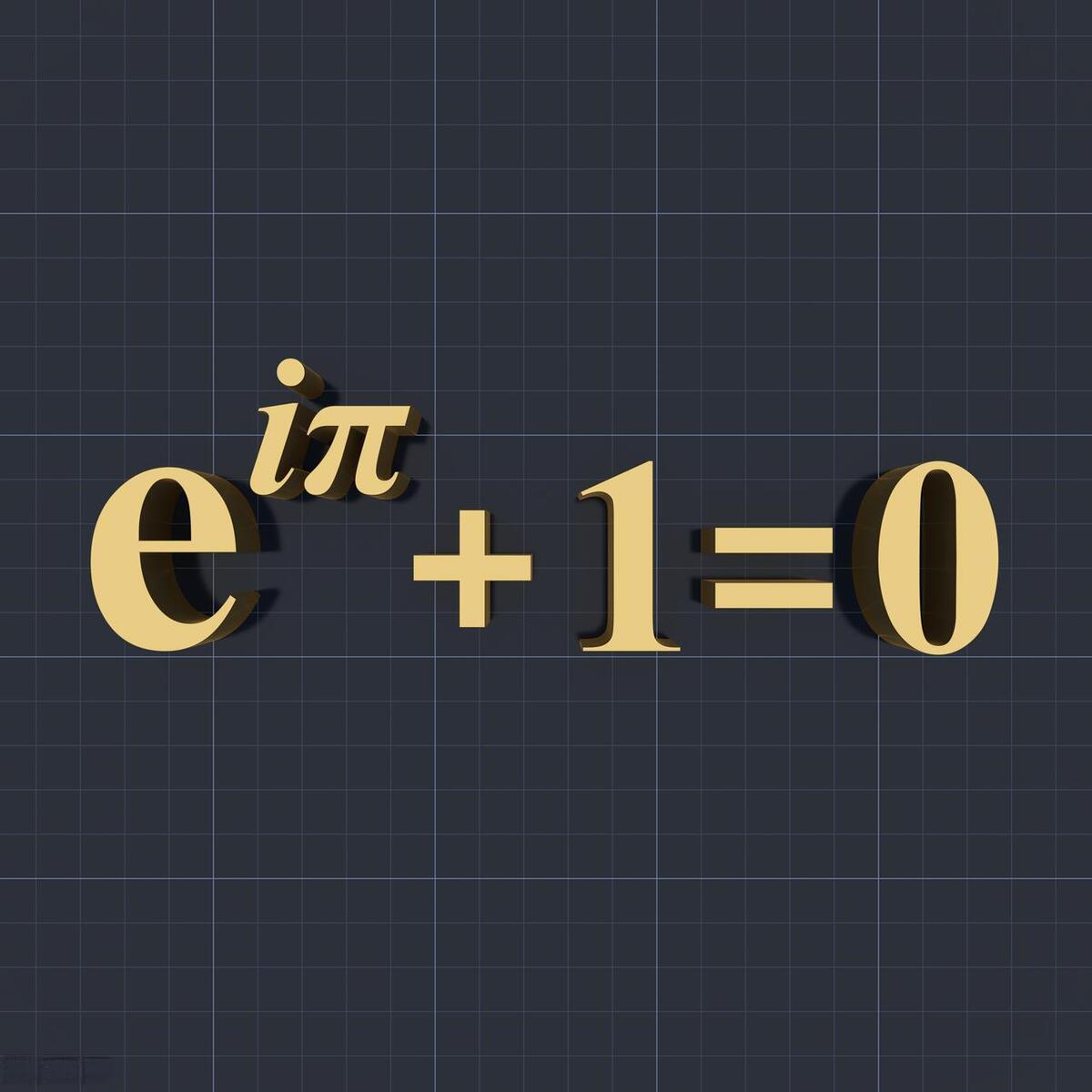
e^iπ + 1 = 0

这个简洁而优美的等式就是著名的欧拉公式，它将数学中几个看似不相关的常数巧妙地联系在一起，被誉为“数学中最优美的公式”。让我们一起揭开这个公式的神秘面纱，探索它背后的数学之美。

欧拉公式中包含了三个重要的数学常数：e、π和i。e是自然对数的底数，约等于2.71828，它在自然界和数学中都有广泛的应用，如描述指数增长过程。π是圆周率，约等于3.14159，它不仅与圆的性质密切相关，还在许多数学和物理问题中扮演重要角色。i是虚数单位，满足i^2 = -1，它的引入使得数学家能够处理负数的平方根问题。

这三个常数通过简单的运算符号（指数、乘法和加法）被巧妙地联系在一起，形成了欧拉公式。这个公式的神奇之处在于，它不仅展示了数学的简洁美，还揭示了这些常数之间深刻的内在联系。

欧拉公式的证明过程同样令人着迷。一个常用的方法是利用泰勒级数展开。我们知道，任何光滑函数都可以用无穷级数来表示。对于指数函数e^x，其泰勒级数展开为：

e^x = 1 + x + x^2/2! + x^3/3! + ...

对于三角函数cos(x)和sin(x)，它们的泰勒级数展开分别为：

cos(x) = 1 - x^2/2! + x^4/4! - ...
sin(x) = x - x^3/3! + x^5/5! - ...

现在，让我们将x替换为iθ，其中θ是一个实数。根据欧拉公式，我们有：

e^(iθ) = cos(θ) + i*sin(θ)

将e^(iθ)的泰勒级数展开，并将i的幂次替换为相应的实数和虚数部分，我们可以得到：

e^(iθ) = (1 - θ^2/2! + θ^4/4! - ...) + i*(θ - θ^3/3! + θ^5/5! - ...)

这恰好与cos(θ)和sin(θ)的泰勒级数展开相吻合，从而证明了欧拉公式的正确性。

欧拉公式的应用范围极其广泛。在数学领域，它被用于复数的表示、傅里叶分析、群论等多个方面。在物理学中，它更是不可或缺的工具，尤其是在描述圆周运动、波动现象和量子力学等领域。正如物理学家理查德·费曼所说，欧拉公式是“我们的珍宝”和“数学中最非凡的公式”。

欧拉公式的美学价值同样不容忽视。它以最简洁的形式展现了数学的和谐与统一，将看似不相关的数学常数联系在一起，揭示了数学世界的深层结构。德国数学家卡尔·弗里德里希·高斯曾说：“如果一个人第一次看到这个公式而不感到它的魅力，那么他不可能成为一流的数学家。”

欧拉公式的发现不仅展示了数学的美妙，也推动了数学的发展。它启发了数学家们去探索更深层次的数学结构，促进了复数理论和复分析的发展。正如法国数学家皮埃尔-西蒙·拉普拉斯所说：“读读欧拉，他是所有人的老师。”

欧拉公式的魅力不仅在于其形式的简洁和内容的深刻，更在于它所体现的数学与自然界的和谐统一。它以数学语言揭示了自然界的基本规律，展现了数学作为“科学的语言”的强大威力。对于每一个热爱数学的人来说，深入理解欧拉公式都是一次美妙的数学之旅，它能激发我们对数学之美的无限向往。