期权交易中的期权价值如何被定价？

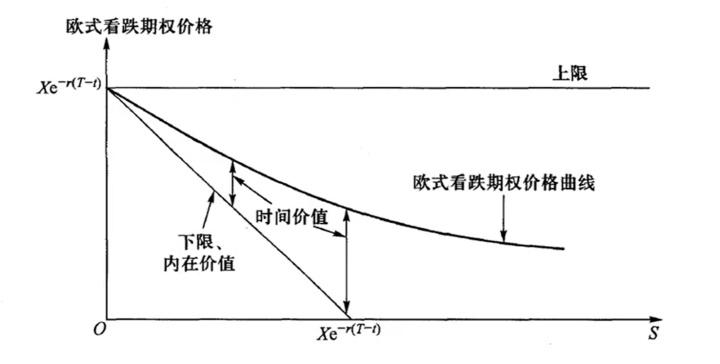
1973年，费雪·布莱克和迈伦·斯克尔斯在《政治经济学杂志》上发表了一篇划时代的论文，提出了著名的Black-Scholes期权定价模型。这一模型为金融衍生品市场的合理定价奠定了基础，也为两位学者赢得了1997年的诺贝尔经济学奖。

Black-Scholes模型的核心公式简洁而优雅，它基于一系列假设条件，包括股票价格服从对数正态分布、无风险利率和金融资产收益变量恒定、市场无摩擦等。模型通过复杂的数学推导，得出了欧式看涨期权和看跌期权的定价公式。这一突破性的成果迅速被芝加哥期权交易所采用，并随着计算机技术的发展而广泛应用。

然而，Black-Scholes模型并非完美无缺。从一开始，学术界就对其假设条件提出了质疑。例如，股价的跳跃式变动、交易成本的存在、股票分红等因素都被模型所忽视。正如罗伯特·默顿所指出的：“股价的变动不仅包括对数正态分布的情况，也包括由于重大事件而引起的跳起情形，忽略后一种情况是不全面的。”

随着时间的推移，越来越多的研究者开始尝试改进和完善Black-Scholes模型。默顿本人就扩展了原模型，使之适用于支付红利的股票期权。其他学者则从不同的角度出发，提出了新的模型和方法。例如，二项式期权定价模型和蒙特卡罗模拟等方法被引入，以应对更复杂的市场情况。

尽管如此，Black-Scholes模型仍然在金融实践中发挥着重要作用。正如一位学者所言：“总体而言，布-肖模型仍是相当准确的，是具有较强实用价值的定价模型。”它的贡献不仅在于提供了一个具体的定价公式，更在于它开创了一种系统化、数学化分析金融衍生品的方法。

期权定价模型的发展历程告诉我们，金融理论的演进是一个不断逼近现实、不断修正和完善的过程。每一个新模型的出现，都是对现有理论的挑战和补充。在这个过程中，我们既要尊重理论的贡献，又要保持批判性思维，不断探索更符合现实的定价方法。

对于投资者和金融从业者来说，理解期权定价模型的局限性同样重要。它提醒我们，任何模型都只是对复杂现实的简化，真正的投资决策还需要结合市场情况、个人风险偏好等多方面因素。正如Black-Scholes模型的创始人所展示的，持续学习、勇于创新，才是应对金融市场变化的不二法门。