拉格朗日中值定理是什么？有什么作用呢？为什么要学习？

拉格朗日中值定理是微分学中的一个基本定理，它揭示了函数在闭区间上的整体变化率与其在区间内某一点的局部变化率之间的关系。这个定理不仅在数学理论中占有重要地位，更在物理学、工程学、经济学等多个领域有着广泛的应用。

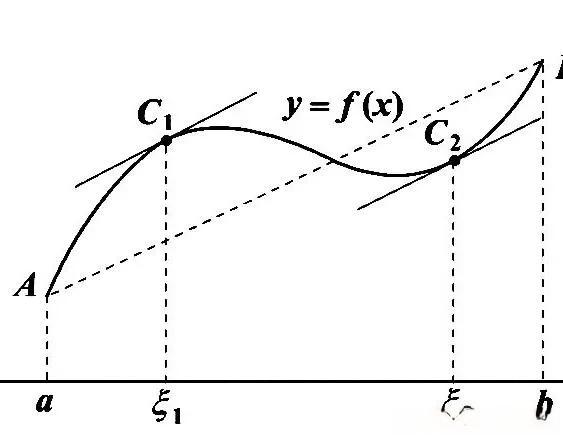
拉格朗日中值定理的数学表述如下：如果函数f(x)在闭区间[a,b]上连续，在开区间(a,b)内可导，那么在开区间(a,b)内至少存在一点ξ，使得f'(ξ) = (f(b) - f(a))/(b - a)。这个等式表明，函数在闭区间上的平均变化率等于其在某一点的瞬时变化率。

在物理学中，拉格朗日中值定理可以用来描述物体的运动。例如，如果我们知道一个物体在t1时刻和t2时刻的位置分别是x1和x2，那么我们可以用拉格朗日中值定理来确定物体在这段时间内的平均速度。更进一步，我们可以找到一个时刻t，使得物体在该时刻的瞬时速度等于这段时间内的平均速度。这个结论对于研究物体的运动规律非常有用。

在工程学中，拉格朗日中值定理可以帮助工程师分析和优化系统性能。例如，在电路设计中，工程师可以利用这个定理来确定电路中某一点的电压变化率，从而优化电路的性能。在机械设计中，这个定理可以用来分析机器零件的应力分布，帮助工程师设计更安全、更高效的机械结构。

在经济学中，拉格朗日中值定理可以用来分析成本函数和收益函数的变化。例如，如果一个公司的总成本函数是C(x)，其中x是产量，那么我们可以用拉格朗日中值定理来确定在产量从x1增加到x2的过程中，总成本的平均变化率。这个结论对于企业制定生产计划和定价策略非常重要。

拉格朗日中值定理的应用远不止于此。在数学分析中，这个定理是证明许多重要结论的基础。例如，它可以用来证明函数的单调性、凹凸性，以及求解极限等问题。在数值分析中，这个定理可以用来估计函数的近似值，从而简化复杂的计算过程。

学习拉格朗日中值定理不仅能够帮助我们解决具体的问题，更重要的是，它能够培养我们的数学思维和解决问题的能力。通过理解这个定理，我们可以学会如何将复杂的问题简化，如何从整体和局部两个角度来分析问题，以及如何将抽象的数学概念应用到实际问题中。

总的来说，拉格朗日中值定理是一个强大而实用的数学工具。它不仅在理论研究中占有重要地位，更在解决实际问题中发挥着重要作用。无论是在科学研究、工程设计，还是在日常生活中，掌握这个定理都能帮助我们更好地理解和分析问题，做出更明智的决策。