一招教你快速搞定百化分

在公务员考试的资料分析部分，有一个看似简单却让许多考生头疼的问题： 如何快速将百分数转换为分数，即所谓的“百化分” 。掌握这一技巧不仅能提高解题速度，还能降低计算错误率。那么，如何快速搞定百化分呢？

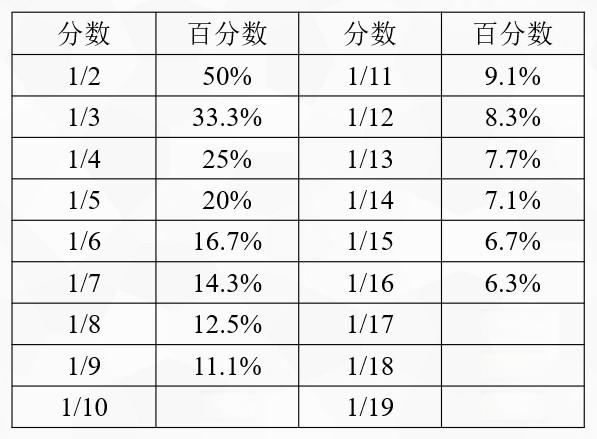
首先，我们需要记住一些常用的百化分。例如， 1/2=50% ， 1/3≈33.3% ， 1/4=25% 等。对于其他分数，我们可以采用“分组记忆法”来快速记忆。例如， 1/9≈11.1% 和 1/11≈9.1% 可以放在一起记忆，因为它们的数值很接近。再比如， 1/17、1/18和1/19可以称为“五点九六三组合” ，因为它们分别约等于5.9%、5.6%和5.3%。

除了记忆，我们还需要掌握一些快速转换的技巧。例如，“整体转化法”可以帮助我们将不熟悉的百分数转化为分数形式。比如，已知1/7≈14.3%，那么1/14.3≈7%。这种方法的关键是将分数的分母和百分数的分子进行调换，但等量关系仍然成立。

另一个实用的技巧是“0的个数固定不变”。例如，1/2=50%，而1/20=5%。我们可以发现，1/20中的20在2的基础上多了一个0，那么5%在50%的基础上就少了一个0。利用这个规律，我们可以快速进行转换。

让我们通过一个例题来看看百化分在实际解题中的应用。假设2010年上半年成品油表观消费量为10963万吨，同比增长12.5%。要求计算2010年上半年全国成品油表观消费量同比增加了多少万吨。按照常规方法，我们需要计算10963×12.5%/(1+12.5%)，这涉及到复杂的乘除运算。但是，如果我们使用百化分，问题就变得简单多了。 12.5%对应的分数是1/8 ，所以 增长量=10963/(1+8)=10963/9=1218万吨 。这个方法只需要一个简单的除法运算，大大提高了解题速度和准确性。

百化分的应用不仅限于增长量的计算。在处理复杂的数据时，它同样能发挥重要作用。例如， 如果遇到一个介于两个已知百化分之间的百分数，我们可以取中间值进行估算 。比如，已知1/9≈11.1%，1/10=10%，那么对于10.6%，我们可以将其视为1/10.5，从而快速进行计算。

要真正掌握百化分技巧，关键在于多加练习。在日常学习中，我们可以尝试将遇到的百分数转换为分数形式，逐渐熟悉各种转换规律。同时，也要注意总结归纳，发现更多有趣的记忆方法和转换技巧。

总之，百化分虽然看似简单，却是提高资料分析解题速度和准确性的有力工具。通过科学的记忆方法和灵活的转换技巧，我们完全可以快速搞定百化分，为公务员考试的成功奠定基础。