三阶魔方复原（图文详解）

三阶魔方，这个看似简单的立方体玩具，背后却蕴含着深奥的数学原理和令人惊叹的复杂性。自1974年由匈牙利建筑学教授鲁比克发明以来，魔方不仅成为风靡全球的益智玩具，更成为数学家和计算机科学家研究的对象。

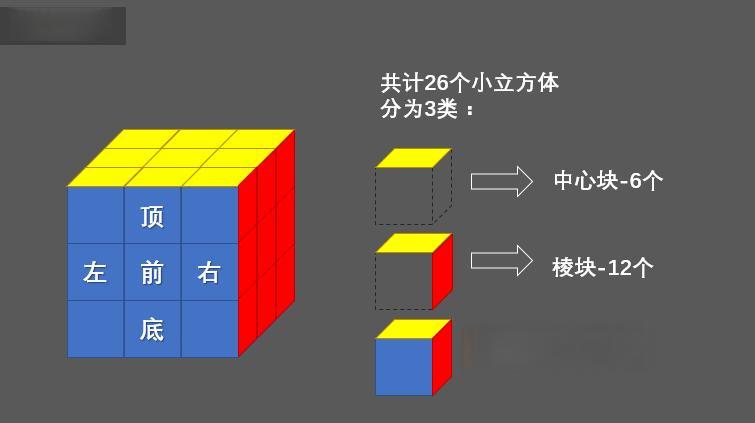
魔方的结构看似简单：一个由26个小块组成的3x3x3立方体。然而，正是这种简单的结构，却能产生令人难以置信的变化。根据数学计算，一个三阶魔方的总变化数高达43,252,003,274,489,856,000种，相当于地球人口的600多倍。

这种惊人的复杂性源于魔方的特殊结构。魔方由8个角块、12个棱块和6个中心块组成。每个块都有特定的位置和朝向，而魔方的转动规则限制了这些块的移动方式。例如，角块只能移动到角块的位置，棱块只能移动到棱块的位置。这种限制使得魔方的解法成为一个复杂的排列组合问题。

魔方的解法原理基于群论这一数学分支。群论研究的是元素集合在某种运算下的性质。在魔方中，这种运算就是转动。每个转动都可以看作是一个元素，而所有可能的转动组合构成了一个群。魔方的解法就是找到一系列转动，使得魔方从任意混乱状态回到初始状态。

基于这种原理，魔方的解法可以分为几个步骤。最常见的是“层先法”，即先还原底层，再还原中层，最后还原顶层。这种方法虽然简单易学，但效率不高。更高级的解法是CFOP法，它将解法分为四个步骤：底层十字、前两层、顶层颜色还原和顶层位置还原。

无论采用哪种方法，魔方的解法都涉及到一系列精心设计的“公式”。这些公式是经过大量实践和理论分析得出的最优解。例如，还原顶层十字的公式是“前顺时针——右手公式：上左下右——前逆时针”。这个公式看似简单，但实际上是在利用魔方的结构特点，通过特定的转动序列来达到目标状态。

魔方的解法不仅是一个数学问题，也是一个计算问题。2010年，科学家们利用强大的计算机算法证明，任意一个三阶魔方都可以在20步内还原。这个数字被称为“上帝之数”，是魔方解法复杂性的极限。

魔方的魅力不仅在于它的复杂性，更在于它激发了人们对数学和算法的兴趣。从简单的玩具到复杂的数学模型，魔方展示了数学之美和人类智慧的力量。无论是作为休闲娱乐，还是作为数学研究的对象，魔方都将继续吸引着人们去探索和挑战。